L'Astronomie, vol. 123, février 2009 n°13, pp. 10-15, ISSN 0004-6302

Troisième dimension : de plus en plus loin dans notre Galaxie

Catherine Turon et Frédéric Arenou

Observatoire de Paris, GÉPI / CNRS UMR 8111

« Toujours la vue des étoiles me fait rêver, aussi simplement que me donnent à rêver les points noirs représentant sur la carte géographique villes et villages. Pourquoi, me dis-je, les points lumineux du firmament nous seraient-ils moins accessibles que les points noirs sur la carte de France ? »

Lettres à Théo, Vincent Van Gogh

Un peu d'histoire

La Grande Ourse, Orion, la Couronne Boréale, l'Aigle. Ces belles constellations sont observées depuis toujours par les hommes, car elles sont faciles à distinguer à l'oeil nu. La première impression est qu'elles sont immuablement dessinées sur une sphère qui entoure la Terre : c'est la Sphère des Fixes des anciens. Est-ce que la Terre est au centre ? est-ce que tout tourne autour d'elle ? Quel est cet Univers que l'on voit autour de nous ? Quelle est sa forme ? sa dimension ? de quoi est-il constitué ? Est-ce qu'il évolue au cours du temps ? Comment s'est-il formé ? Est-ce que toutes ces étoiles sont toutes à la même distance de la Terre ? Autant de questions qui intriguent les humains depuis la nuit des temps.

Dès les 6^ème et 5^ème siècle avant J.-C., les mathématiciens et philosophes grecs, qui étaient aussi astronomes, se préoccupaient d'observer et d'interpréter les mouvements des astres. Pythagore de Samos (~575-~495 avant J.-C.) fut l'un des premiers à comprendre que l'astre le plus lumineux après le Soleil et la Lune, l'étoile du soir ou du matin, était en fait un même et unique objet (Vénus !). Les mouvements des planètes sur la Sphère des Fixes sont observés en détail dès cette époque, et Eudoxe de Cnide (~410-~350 avant J.C.), disciple de Platon, est le premier à concevoir un modèle mathématique susceptible de les expliquer : outre la sphère des Fixes, un emboîtement centré sur la Terre de trois sphères concentriques pour le Soleil, autant pour la Lune et quatre pour chacune des cinq planètes connues. Aristarque de Samos (310-~230 avant J.-C.), parallèlement à ses travaux sur la mesure des distances et diamètres de la Lune et du Soleil, fit déjà deux hypothèses essentielles : la Terre tourne sur elle-même, ce qui explique fort simplement la succession des jours et des nuits, et la Terre tourne autour du Soleil et non l'inverse. L'argument essentiel de ses détracteurs (hormis le caractère impie de vouloir mettre la Terre ailleurs qu'au centre du Monde) était que si la Terre se déplaçait autour du Soleil, on devrait voir les étoiles dans des directions différentes au cours des saisons. Mais la réponse d'Aristarque, prétendant que si on ne voyait pas ces déplacements c'est que les étoiles étaient très lointaines, ne les convainquait pas. Ce qui est tout à fait remarquable, c'est que tous ces raisonnements étaient le fruit d'une démarche scientifique rigoureuse pour tenter de comprendre la nature et la structure de l'Univers à partir de l'observation des mouvements des astres et de théories mathématiques permettant de les interpréter. La découverte des différents mouvements qui animent les étoiles fixes a dû attendre la mise au point du télescope avec Galilée, et a ensuite été très progressive. Il a fallu attendre le milieu du 19^ème siècle pour que les progrès instrumentaux permettent les premières mesures de parallaxes trigonométriques. Voir Encadré 1.

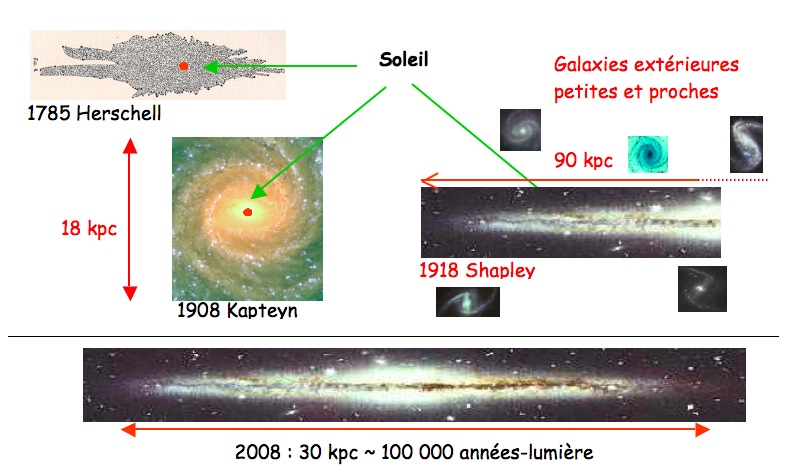
On peut faire un parallèle saisissant entre la compréhension de la structure, des distances et des mouvements dans le Système Solaire avec celle de notre Galaxie : Herschel en tenta une carte en 1785 et il a fallu attendre les années 1930 pour établir que le Soleil n'était pas au centre de celle-ci, et pour en déterminer la forme (encore approchée !) et la dimension. En dehors de la difficulté à nous imaginer ailleurs qu'au centre du Monde – que le Monde soit le Système Solaire ou la Galaxie – il y a un point commun entre ces deux problèmes scientifiques : un manque criant de mesures précises des distances des objets considérés.

La distance des étoiles

Il est intéressant de voir que beaucoup des astronomes dont l'histoire a retenu le nom ont tenté de donner un ordre de grandeur à la « distance des étoiles ». La Table 1 en donne une sélection, ainsi que la comparaison des premières mesures de distances avec les distances obtenues par le satellite Hipparcos.

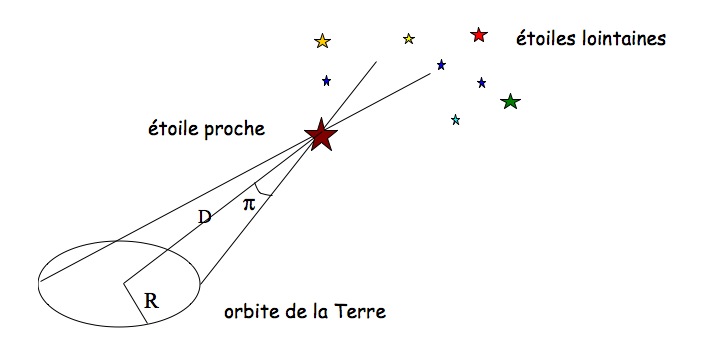
Newton a obtenu la distance de Sirius par comparaison de la magnitude de Sirius avec celle de Saturne ; la fraction de la lumière réfléchie par Saturne, supposant connus le rayon de celle-ci, sa distance au soleil et son albedo, indique la distance à laquelle il faudrait repousser le Soleil pour qu'il ait la magnitude apparente de Saturne. Bessel, Struve et Henderson sont les auteurs des premières mesures de parallaxes trigonométriques.

Le principe de la mesure d'une parallaxe trigonométrique est expliqué dans l'encadré n°2. Les difficultés sont multiples :

-  Tout d'abord les quantités à mesurer sont extrêmement petites car il se trouve que le Soleil est dans une zone peu peuplée de notre Galaxie. L'étoile la plus proche est à 1,3 pc (soit 4,2 années-lumière) avec une parallaxe trigonométrique de 0,77 seconde de degré (la seconde de degré est notée " ci-dessous), et il n'y a que 50 étoiles à moins de 5 pc, avec une parallaxe trigonométrique plus grande que 0,2". Pour se rendre compte à quel point ces quantités sont petites, il faut s'imaginer observer une myrtille située à un km, et essayer de distinguer le trajet effectué par un moucheron allant d'un côté à l'autre de la myrtille en une année ! Ceci est équivalent à mesurer une parallaxe trigonométrique de 1", soit une étoile située à une distance de 1 pc. Une milliseconde de degré (notée mas ci-dessous), la précision du satellite Hipparcos, est l'angle sous lequel on verrait un personnage sur la Lune. Enfin, une microseconde de degré (notée μas ci-dessous), est l'angle sous lequel on verrait le pistil d'une fleur sur la Lune ou un rosier sur Mars  La précision espérée pour Gaia pour les étoiles les plus brillantes (jusqu'à la magnitude 13) est de 7 μas.

-  Une deuxième difficulté vient du fait que le mouvement dû à l'effet de parallaxe trigonométrique n'est, de loin, pas le seul qui perturbe la position des étoiles sur la Sphère des Fixes. Elles sont, en particulier, animées d'un mouvement par rapport au Soleil. Sa projection sur la Sphère Céleste est le mouvement propre (sa projection sur la ligne de visée est la vitesse radiale).

-  Une troisième difficulté tient au fait que de nombreuses étoiles font partie de systèmes doubles ou multiples, et que chacune des composantes de tels systèmes tourne autour du centre de gravité du système, ce qui se traduit par autant de mouvements sur la Sphère Céleste.

-  Enfin, la quantité physique recherchée est la distance de l'étoile observée. Elle permet de placer l'étoile dans la Galaxie et, par comparaison avec son éclat apparent, de déterminer sa luminosité intrinsèque. 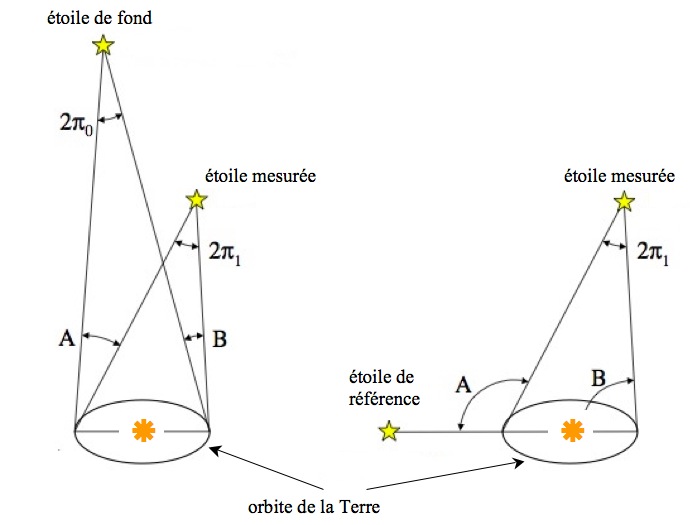Au sol, les observations sont effectuées dans de petits champs, et on obtient la parallaxe relative de l'étoile observée, c'est à dire la distance de l'étoile comparée à celles des quelques étoiles qui l'entourent dans le champ de l'instrument, étoiles que l'on suppose très lointaines. Avec des satellites comme Hipparcos et Gaia, les deux champs d'observation, séparés par un grand angle sur la Sphère Céleste, permettent de mesurer directement de grands angles et d'obtenir une parallaxe absolue, donc la distance réelle de l'étoile.

En conséquence de toutes ces difficultés, la qualité et le nombre de mesures de parallaxes trigonométriques ont très lentement progressé depuis les trois mesures pionnières de Bessel, Hendersen et Struve jusqu'à l'avènement des mesures astrométriques dans l'espace, ou astrométrie spatiale. Ceci est montré dans la Table 2. Les deux sauts quantitatifs correspondent à l'avènement des méthodes photographiques au début du vingtième siècle puis à celui de l'astrométrie spatiale. Dans les années 1980, les techniques photographiques, bien qu'ayant fortement progressé, avaient montré leurs limites : en une année (1984), l'Observatoire de Flagstaff avait obtenu 50 mesures. A ce rythme, il aurait fallu 2000 ans pour obtenir des mesures pour autant d'étoiles qu'avec le satellite Hipparcos en 3 ans, et de plus elles auraient été moins précises.