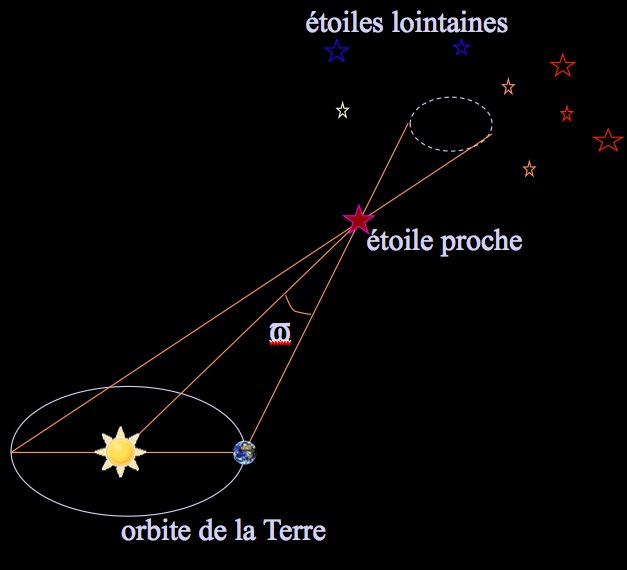
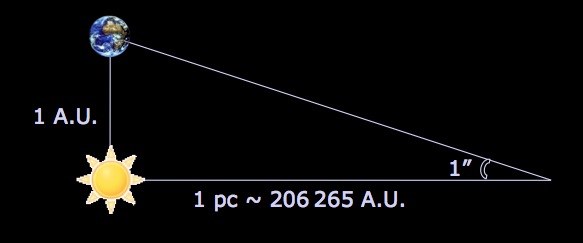
En 1913, Herbert Hall Turner invente le mot-valise « parsec » (PARallaxe d'une SEConde d'arc) pour caractériser une unité de distance d'étoiles. Cette unité est définie comme la distance à laquelle l'unité astronomique (la « distance moyenne » Terre-Soleil) serait vue sous un angle d'une seconde de degré. La magnitude absolue M, quant à elle, est définie en fonction de la magnitude apparente m et de la distance dpar M = m - 5 log(d/10 pc). Ces définitions un peu compliquées sont le fruit de compromis pour régler trois problèmes entremêlés au début du XX^ème siècle: quelle unité de distance stellaire adopter? Quel nom lui donner? Comment définir une magnitude absolue, de manière à pouvoir comparer les magnitudes qu'auraient différentes étoiles à une même distance donnée?

Sirius, l'étalon

Avec une certaine logique, l'unité de distance des étoiles intervient lors des premières études sur l'astronomie galactique effectuées par ce précurseur que fut William Herschel à la fin du XVIII^ème siècle. Quand il décide de « sonder » notre Galaxie pour déterminer sa forme, connaître précisément les distances des étoiles est encore hors de portée, car les premières parallaxes précises ne seront en effet mesurées que plus d'un demi-siècle plus tard. Herschell décide donc d'utiliser la distance de Sirius, en tant que représentant de la distance moyenne des étoiles de première magnitude, comme unité de distance. Ceci, sous l'hypothèse (certes inexacte, comme celle qui voudrait que les étoiles seraient toutes de même magnitude absolue) que les étoiles « de deuxième magnitude sont à deux fois cette distance, celles de troisième magnitude à trois fois cette distance, etc. » (Herschel, 1785). Incidemment, on peut noter que la distance de Sirius n'est pas complètement inconnue à l'époque de Herschell: Gregory en 1668, Huygens en 1698, et surtout Newton en 1685, en ont obtenu une estimation photométrique finalement pas si éloignée de la valeur contemporaine, mais, bref, Sirius joue ici seulement le rôle d'étalon de distance.

L'évolution des idées

Avant même que des distances stellaires puissent enfin être rigoureusement déterminées (autour de 1838 par Bessel, Struve et Henderson), on sait déjà que les parallaxes sont inférieures à la seconde de degré, indiquant ainsi l'immensité des distances des étoiles au soleil et l'inadéquation des unités de mesure usuelles. La vitesse de la lumière est également connue, et, comme l'indique Bode (1768), plus que la distance parcourue à la vitesse d'un boulet de canon, « il existe dans la nature une mesure beaucoup plus grande pour déterminer la prodigieuse distance des étoiles fixes, sans être obligé de trop multiplier les nombres : c'est la marche de la lumière ». Il n'est d'ailleurs pas le premier à utiliser cette comparaison: en 1694, Roberts indique déjà que « la lumière mets plus de temps à venir depuis les étoiles que nous à voyager vers les Caraïbes ».

Exprimer les distances stellaires en unités d'années de lumière n'est pas donc pas inhabituel, et ce, dès avant la fin du XVIII^èmesiècle. Quand il expose dans ses cours les premières déterminations des quelques (8) parallaxes annuelles connues à ce moment-là (avant 1846), Arago indique leur parallaxe, leur distance à la terre en Unités Astronomiques et en lieues, mais il prend soin d'également produire un second tableau en années (de lumière). De même, Flammarion (1865) donne une idée de la distance d'étoiles en utilisant la durée du trajet des rayons lumineux (« la lumière ne met pas moins de 22 ans pour nous venir de Sirius »). Quant au nom « année-lumière » (anciennement: « année de lumière » dont l'usage est recommandé), la date d'apparition de son premier usage n'est pas évident. Si les livres d'astronomie semblent y faire référence seulement à la fin des années 1880, on peut cependant trouver au moins dès 1868 ce mot dans le vocabulaire anglais (par ex. Fay, 1868).

Une unité très peu unie

Pourtant, bien après (au début du XX^ème siècle), on voit apparaitre dans plusieurs articles scientifiques, outre l'année-lumière, d'autres unités de distance, baptisées de noms variés. Kobold (1906) définit une « Sternweite » (distance stellaire), une distance correspondant à une parallaxe d'une seconde d'arc. En 1909, Seeliger définit une « Siriusweite » (distance de Sirius, renouant ainsi avec Herschel), en lui attribuant une parallaxe de 0.2" (soit 1.03 10⁶ unités astronomiques), une unité qu'il a déjà utilisée comme référence dans son étude fondamentale sur la statistique stellaire de 1898. Quant à Charlier (1913), il indique qu'il utilise le terme « siriomètre » depuis deux ans, avec comme définition 10⁶ unités astronomiques exactement. En 1912, Turner, dont on reparlera plus loin, utilise les années-lumière comme unité de distance pour des étoiles de type A (p. 482), mais; deux pages plus loin, il utilise une unité correspondant à une parallaxe de 1" sans lui donner de nom. Bref, la confusion règne.

C'est d'autant plus problématique que le début du XX^ème siècle est en effet le moment où les données de mouvements propres, et dans une moindre mesure des parallaxes dont ils servent parfois de substitut, commencent à permettre l'étude de la « structure de l'univers » comme l'écrit Kapteyn. Ses recherches, dont il est précurseur avec Seeliger, et ils sont bientôt suivis par de nombreux autres, visent en effet à déterminer en substance la distribution spatiale des étoiles de différents types, mouvements propres, magnitudes absolues et distances.

Comme on l'a indiqué, l'utilisation de l'unité de distance (quel que soit son nom) a également une incidence directe sur la définition de la magnitude absolue. Pour pouvoir comparer des étoiles de différents types, il y a en effet besoin d'utiliser une définition de luminosité qui soit intrinsèque. Puisque la luminosité décroît avec le carré de la distance, et que la magnitude apparente est définie comme 2.5 fois une échelle logarithmique en fonction du flux reçu, l'écart entre magnitudes apparente et absolue vaut 5 fois le logarithme de la distance, à une constante près... dépendant de l'unité de distance utilisée. Ainsi, quand il entreprend de comparer les luminosités intrinsèques des étoiles, Hertzsprung (1913), dans sa calibration des céphéides, prend 1 parsec comme référence, tout comme Eddington (1914). En revanche, Plummer (1912) utilise une « magnitude intrinsèque » utilisant 100 pc comme référence! Pourtant, depuis plusieurs années, Kapteyn (1902, 1910) a introduit clairement la définition actuellement utilisée… mais, de façon cohérente, avec une unité de distance correspondant à une parallaxe de 0.1''. Auparavant, Seeliger a déjà utilisé une luminosité absolue rapportée à la distance de Sirius. Il devient donc plutôt difficile de s'y retrouver, faute de coordination.

Le débat

C'est à ce moment qu'intervient l'origine du nom « parsec ». Dans une étude où il utilise comme unité de distance celle correspondant à une parallaxe d'une seconde, Dyson (1913) indique dans une note de bas de page, la nécessité de nommer l'unité de distance. Il préconise « astron » et mentionne que H. Turner a suggéré « parsec », probablement suite à la lecture d'une version préliminaire de cet article. Le débat est lancé. Une discussion s'engage d'ailleurs peu après à la Royal Astronomical Society: après la présentation de l'Astronome Royal (Dyson, 1913b), Turner (p. 167) revient sur la question de la désignation de l'unité de distance. Pour lui, « astron » sonne comme « unité astronomique », et (après avoir proposé « parsec ») il suggère maintenant également « macron ». Dyson (p. 168) répond que « Siriomètre » fait penser à une machine à mesurer, qu'il avait également pensé à « macron » jusqu'à ce qu'il craigne que la signification de « micron » prête à confusion.

Le consensus ne règne donc pas encore, loin de là. Paddock (1913) résume les différentes désignations proposées, et rappelle que, pour compliquer encore les choses « en discutant de la distance des nébuleuses, le Professeur Very propose comme unité la distance d'Andromède, et comme nom '' andromede '' ». Quant à lui, il inclinerait plutôt pour « astron » ou « astrometer ».

En réponse, dans le même numéro de cette revue (PASP), Curtis (1913) se fend d'un article, soutenant qu'une unité reposant sur des constantes fondamentales, comme la vitesse de la lumière, serait préférable. Avec un deuxième argument: aucune des autres unités proposées n'est connue parfaitement: l'unité astronomique n'est pas mieux connue (à l'époque) qu'au millième, la parallaxe mesurée pour Sirius varie entre 0.34 et 0.40, et la nébuleuse d'Andromède sans doute pas mieux qu'à 50% (le futur montrera que c'est 160000%!). Curtis soutient également qu'une unité ne doit pas servir uniquement au spécialiste mais également au non-initié, Enfin, il ne voit pas bien l'avantage de mentionner une distance d'étoile à 14.3 parsecs plutôt que d'indiquer que sa parallaxe vaut 0.07 secondes. En plein débat sur la taille de notre univers visible, Curtis ajoute « que la Voie Lactée soit de trois mille ou de plusieurs millions d'années-lumière de longueur, l'année-lumière reste une unité utilisable ».

Ce n'est pas l'avis d'Eddington (1914) qui regrette que « l'année-lumière, malgré ses inconvénients et le manque de pertinence, a parfois glissé de l'usage populaire aux études techniques ». Il faut ainsi remarquer qu'aucun motif argumenté n'est avancé pour rejeter l'utilisation de l'année-lumière sinon que Dyson (1913b) « pense que l'utilisation de l'année-lumière a été introduite pour des conférences, pas de manière opérationnelle quand votre auditoire travaille avec des étoiles ».

L'U.A.I. normalisateur

Le parsec est rapidement adopté par Eddington (1914) dans son ouvrage sur les mouvements stellaires. En 1919, la (naissante, et maintenant défunte) Commission « Notations » de l'Union Astronomique Internationale (UAI) suggère l'utilisation de l'année-lumière « surtout dans les articles populaires », et du parsec, « ou de préférence une unité dix fois plus grande avec un nom distinct » (Campbell, 1920). À la même époque, Kapteyn (1920) prend acte de l'utilisation du parsec « très pratique (bien que très laid) » et propose donc maintenant de définir la magnitude absolue à 1 et non plus 10 parsecs! En 1922, la Commission 3 de l'UAI décide de l'utilisation des notations m et M pour les magnitudes apparente et absolue, et l'utilisation du parsec, mais sans la restriction précédente. En 1925, l'UAI confirme ces unités. Ce qui ne signifie pas qu'il y ait unanimité: dans le journal 'the Observatory', Malmquist (1925) s'y refuse et il a beau jeu de noter que l'unité de distance est le parsec, tandis que la définition de la magnitude absolue ne repose pas sur le parsec mais sur le multiple de celui-ci… Il suffit d'ailleurs de feuilleter ce même journal pour constater que le parsec n'est pas encore d'un usage courant douze ans après sa proposition: c'est en années-lumière que Doig (p. 138) exprime les dimensions de M31 et M33 ou la distance d'amas ouverts. Et, dans l'article précédent (p. 142), celui qui signera la « fin de l'univers de Shapley », Hubble (1925) utilise bien le parsec mais précise sa traduction en années-lumière.

À l'assemblée suivante de l'UAI, Charlier (1928) n'a pas baissé les bras. Comprenant les réticences concernant le « siriomètre » qu'il avait proposé (et indiquant au passage que des astronomes français auraient suggéré « Herschel » comme nom), il propose comme unité de distance stellaire: 10⁶ unités astronomiques; comme unité de temps: 10⁶ années tropiques; et la magnitude absolue comme la magnitude à la distance proposée. En tant que président de la Commission 33 de Statistique Stellaire, il compte obtenir le vote d'une résolution de sa Commission à l'adresse de la Commission des notations (p. 260). Il ne sera appuyé que par Malmquist (signalons que ce dernier avait été son étudiant...). La brillante école de Lund est cependant peu soutenue: Russel, Lundmark signalent le désavantage de modifier des unités maintenant bien utilisées dans la littérature existante. À la remarque de Malmquist sur la contradiction entre la définition du parsec et celle de la magnitude absolue, Eddington fait remarquer qu'en physique on utilise bien le litre égal à un décimètre cube... Bref, les propositions de Charlier ne seront donc pas adoptées.

Les conséquences

Pourtant, très rapidement, la plupart des distances d'étoiles ne deviennent connues qu'indirectement, et non par une mesure angulaire de parallaxe annuelle. En effet, la parallaxe des étoiles proches permet par exemple des calibrations de magnitudes absolues d'étoiles de chaque type spectral, et l'utilisation ultérieure de ces calibrations pour des étoiles plus lointaines et sans parallaxes donne lieu, encore de nos jours, à l'expression surprenante de « parallaxes spectroscopiques  ». De même, on utilise également le gigaparsec pour des objets pour lesquels il s'écoulera beaucoup de temps avant que la technologie permette la mesure d'une parallaxe annuelle d'un milliardième de seconde! C'est pourtant le parsec, c'est à dire une unité tirant son origine de la méthode de mesure utilisée (comme le pied ou le pouce!), ce « portmanteau-name » (Eddington) qui est resté utilisé. Peut-être parce c'est un « un mot brillant » (Malmquist). Quant à la magnitude absolue, c'est parce que sa définition avait l'antériorité et qu'elle était utilisée par une majorité d'astronomes. En définitive, l'unité « parsec » aura donc d'abord été utilisée par Kobold, puis son nom inventé par Turner, tandis que Kapteyn a sans doute le premier défini la magnitude absolue telle qu'elle est maintenant utilisée.

• Un parsec = 3.0857 10¹³ km
• Un macron = un astron = une Sternweite = un parsec
• Une année-lumière = 0.3066 parsec
• Un Siriusweite = 5 parsecs
• Un siriomètre = un Herschel = 4.8482 parsecs
• Un Andromède = 490 parsecs (pour Very en 1911; vraie distance ~ 778000 pc!)

• Arago F., 1854, Astronomie populaire, Tome premier, p. 437
• Bode J. E., 1768, Anleitung zur Kenntnis des gestirnten Himmels, p. 653 de l'édition de 1778
• Campbell W. W., Stebbins J., 1920, Report on the Organization of the International Astronomical Union, Proceedings of the National Academy of Sciences of the United States of America, Volume 6, Issue 6, p. 361, 1920PNAS....6..349C
• Charlier, C. V. L., 1913, Stars, Motions and distances, An investigation on the motion of the stars, Monthly Notices of the Royal Astronomical Society, Vol. 73, p. 490, 1913MNRAS..73..486C
• Charlier C., 1928, Report of Commission 33, Transactions of the IAU Vol. III B, Proceedings of the 3rd General Assembly, Leiden, The Netherlands, Ed. F.J.M. Stratton, Cambridge University Press, p. 197
• Curtis H. D., 1913, The Unit of Stellar Distance, Publications of the Astronomical Society of the Pacific, Vol. 25, No. 149, p.213, 1913PASP...25..213C
• Dyson F. W., 1913a, "The distribution in space of the stars in Carrington's Circumpolar Catalogue, Monthly Notices of the Royal Astronomical Society, Vol. 73, p.342, 1913MNRAS..73..334D
• Dyson F. W., 1913b, March 14 meeting of the Royal Astronomical Society, The Observatory, Vol. 36, p. 168, 1913Obs....36..160
• Eddington A. S., 1914, Stellar movements and the structure of the universe, Macmillan and co., p. 14
• Fay T. S., 1868, Great outline of geography for high schools and families, text book, New York, Putnam & sons
• Fernie J. D., 1970, The Historical Quest for the Nature of the Spiral Nebulae, Publications of the Astronomical Society of the Pacific, Vol. 82, No. 490, p.1208, 1970PASP...82.1189F
• Flammarion C., 1865, La pluralité des mondes habités, Gauthier-Villars, p. 192
• Herschel W., 1784, On the Construction of the Heavens, Philosophical Transactions of the Royal Society of London, Vol. 75, p. 217, 1785RSPT...75..213H
• Hertzsprung E., 1913, Über die räumliche Verteilung der Veränderlichen vom _ Cephei-Typus, Astronomische Nachrichten, volume 196, p.201 (AN Homepage), 1913AN....196..201H
• Hubble E. P., 1925, Observatory 48, 139, 1925Obs....48..139H
• International Astronomical Union, Cambridge, 1925 June 14-22, The Observatory, Vol. 48, p. 250, 1925Obs....48..241
• Kapteyn J. C., 1902, On the Luminosity of the fixed stars, Publications of the Kapteyn Astronomical Laboratory Groningen, vol. 11, p. 12, 1902PGro...11....1K
• Kapteyn J. C. & Weersma H. A., 1910, List of parallax determinations, Publications of the Kapteyn Astronomical Laboratory Groningen, vol. 24, p. 16, 1910PGro...24....1K
• Kapteyn J. C. & van Rhijn P. J., 1920, On the Distribution of the Stars in Space Especially in the High Galactic Latitudes, Astrophysical Journal, vol. 52, p. 23, 1920ApJ....52...23K
• Kobold H., 1906, Der Bau des Fixsternsystems, ISBN 0559029136, 9780559029134, p. 74
• Paddock G. F., 1913, Astracts from astronomical publications: The astronomical unit of distance, Publications of the Astronomical Society of the Pacific, Vol. 25, No. 149, p. 221
• Plummer H. C. K., 1912, On the motions of the brighter stars of class A in relation to the Milky Way, Lick Observatory bulletin, no. 212, p.38, 1912LicOB...7...30P
• Roberts F., 1694, Concerning the Distance of the Fixed Stars, Philosophical Transactions, Volume 18, p.103, 1694RSPT...18..101R
• Seeliger H., 1909, Über die räumliche Verteilung der Sterne, Astronomische Nachrichten, volume 182, p.229, 1909AN....182..229S
• Turner H. H., 1912, Stars, Motions in space and the two-drift theory, A tentative explanation of the "two star streams" in terms of gravitation, second note, Monthly Notices of the Royal Astronomical Society, Vol. 72, p. 484, 1912MNRAS..72..387T
• Turner H. H., 1913, March 14 meeting of the Royal Astronomical Society, The Observatory, Vol. 36, p. 167, 1913Obs....36..160
• Very F. W., 1911, Are the White Nebulae Galaxies, Astronomische Nachrichten, volume 189, p.441, 1911AN....189..441V

---