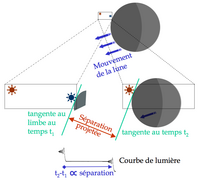
Double à occultation

(La version rédigée pour Wikipédia est ici)

Mesure d'occultation d'une étoile double

Historique

Antarès, le rival de Mars, semble avoir le privilège d'être la première double à occultation détectée. Le couple aurait d'ailleurs pu conserver longtemps son secret, si la chance n'avait pas souri à un certain professeur Burg à Vienne, le 13 avril 1819: « À 12h03mn17.1s, j'ai observé l'émersion d'une étoile de 6.7 mag, qui, après environ 5 secondes m'est soudain apparue comme une étoile de première magnitude... Peut-être qu'Antarès est une étoile double, et la petite observée en premier est si proche de l'étoile principale que les deux, même vues avec un bon télescope, n'apparaissent pas séparées. » [4]. S'il ne fut pas cru à cette époque, l'hypothèse de la réfraction d'une « atmosphère lunaire » étant privilégiée [13], la duplicité d'Antarès fut finalement confirmée par O.M. Mitchel le 13 juin 1846 avec la lunette toute neuve de Cincinnati [1]. Toujours d'après White [13], c'est John Herschel qui émit, en 1833, la suggestion que les mesures d'occultations pouvaient apporter à la détection d'étoiles doubles une haute résolution dont étaient dépourvues les observations classiques.

Les mesures d'occulation peuvent paraître simples, mais en observant attentivement la courbe de lumière on peut noter de curieuses oscillations au moment de l'immersion ou de l'émersion de l'étoile, qui nécessitent un petit détour historique à propos de l'occultation en général, car inséparable de celui de la détection des doubles.

L'observation d'occultations stellaires est sans doute aussi vieille que l'humanité, mais une des plus anciennes mentions qui soient rapportées semble se trouver dans l'Almageste [14]; la première indication (plus ou moins) utilisable de l'instant d'une occultation stellaire attendra le 5 juillet 1623: c'est (Spica) observée à Paris par Ismaël Boulliau, avec un télescope, mais sans horloge [10]. De nombreuses observations ont eu lieu ensuite. Certains observateurs, et non des moindres, voyaient une variation de vitesse apparente au moment des occultations, et des questions d'optique, voire physiologiques étaient invoquées [7]; il faut rappeler que la question se posera longtemps (jusqu'au début du vingtième siècle) de l'existence ou non d'une atmosphère sur la Lune. L'Astronome Royal Airy suggéra que l'effet observé était dû à l'accumulation d'anneaux de diffraction de la lumière lunaire sans pouvoir évidemment le prouver [2]. Eddington (1909) semble être le premier à prendre en compte simplement l'effet de la diffraction de la lumière de l'étoile [5], mais la première mesure expérimentale suffisamment rapide pour mettre en évidence cette diffraction attendra Arnulf: occultation de Régulus, le 6 avril 1933 à l'Observatoire de Paris, sur le télescope de 1m du site de Meudon [14].

Intensité reçue après diffraction par un bord d'écran.

En effet, au premier ordre, l'occultation d'une étoile par la Lune peut se modéliser par une diffraction par un bord d'écran: le bord lunaire joue le rôle du demi-plan, éclairé par la lumière de l'étoile supposée à l'infini. Cet effet est d'abord mentionné, non pas en relation avec la mesure des étoiles doubles, mais vis-à-vis de celle, au moins aussi importante à l'époque comme maintenant, des diamètres stellaires. MacMahon (1908) avait en effet suggéré, de manière purement géométrique, d'estimer des diamètres à l'aide de mesures rapides photographiques lors d'occultations [8], mais Eddington avait vivement répliqué le mois suivant que cette mesure serait inutilisable pour la plupart des étoiles car limitée par la diffraction [5]. De plus, les deux argumentaient que l'irrégularité de la surface lunaire limiterait les mesures. En réalité, les franges de diffraction contiennent l'information que l'objet n'est pas ponctuel, et de nombreuses mesures de diamètres ont été possibles depuis, et ceci sans trop de perturbations sensibles dues à la surface lunaire [6]: en 1987, il y avait 346 mesures de diamètre pour 124 étoiles [14].

Des observations intensives ont eu lieu pendant les années 1970, en particulier par D. S. Evans, puis ensuite dans le proche infrarouge. On estime qu'environ 10% des observations d'occultation peuvent amener à la découverte de la duplicité de l'objet [12]. Le catalogue des doubles à occultation de Mason (1995) contient 772 mesures pour 357 systèmes [9].

La meilleure façon de voir le faible compagnon de la binaire visuelle Aldébaran est pendant une occultation.

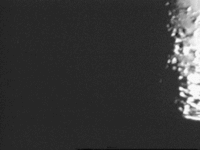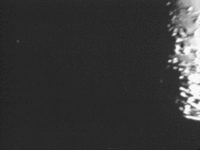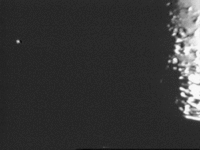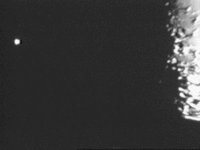
Capacités de la méthode

La plus ancienne des techniques de haute résolution angulaire, cette méthode reste toujours utilisée grâce à ses performances, et est bien adaptée à la découverte systématique d'étoiles doubles, sur lesquelles d'autres techniques plus coûteuses peuvent ensuite se pencher. La méthode d'occultation a en effet plusieurs avantages [11, 12]:

• ni la turbulence atmosphérique (hormis la scintillation), ni la diffraction du télescope ne perturbe trop la mesure: la diffraction est effectuée en amont, par la Lune, dans le vide, et le télescope ne sert qu'à collecter la lumière;
• la résolution angulaire n'est pas directement liée au diamètre de l'instrument, mais bien sûr le rapport signal/bruit l'est; un signal/bruit > 10 est suffisant pour détecter des doubles de séparation > 5 millièmes de seconde d'arc et de différence de magnitude < 1.5 [11];
• le faible coût et la simplicité en termes d'observation et de réduction de données ne réservent pas cette méthode à des astronomes professionnels disposant de grands équipements;
• il n'y a besoin que de peu de temps d'observation;

mais elle a également plusieurs contreparties:

• tout d'abord, seules les étoiles au voisinage de l'écliptique peuvent être observées: le parcours de la Lune ne couvre que 10% du ciel seulement. Les occultations par des astéroïdes apportent une meilleure couverture du ciel mais la prédiction des occultations est plus complexe: les positions doivent être connues précisément compte tenu de la faible dimension apparente des astéroïdes;
• l'observation de la duplicité n'est pas répétable (vérifiable) par cette méthode, sauf à attendre ~18.5 ans;
• une seule mesure du temps séparant les deux évènements ne suffit pas à elle toute seule à obtenir la séparation et l'angle de position du couple. La séparation mesurée n'est pas la vraie séparation du couple, mais la séparation projetée: on obtient une mesure unidimensionnelle seulement, perpendiculairement à la tangente au limbe lunaire. Néanmoins, des mesures faites simultanément en d'autres points du globe terrestre permettent de circonvenir ce problème;
• la méthode est limitée à une faible différence de magnitude (~3.5) entre composantes serrées;

Paramètres

L'utilisation des occultations stellaires vise à résoudre des couples serrés. Si le couple peut être ainsi résolu, et si c'est un couple physique, voir à binaire visuelle comment les masses peuvent éventuellement être obtenues à l'aide de données complémentaires (spectroscopiques).

La vitesse angulaire du mouvement relatif de la Lune est autour de 0.5"/s. Si l'on veut obtenir des mesures à haute résolution, il faut donc échantillonner à environ 1000 mesures par seconde. La durée de pose étant donc très courte, cette méthode favorise les étoiles les plus brillantes.

Une fois les données obtenues, une méthode usuelle [12] est d'ajuster un modèle aux observations, modèle contenant les paramètres suivants:

• les diamètres des composantes,
• leur séparation (projetée),
• la magnitude de chacune des composantes,
• la vitesse relative du limbe,
• le niveau du fond de ciel.

Dans le meilleur des cas (observation à l'immersion et à l'émersion, avec un filtre différent pour chaque), on pourrait donc en théorie obtenir les diamètres, les magnitudes et les couleurs des composantes, ainsi que l'angle de position et la séparation entre elles [11].

Bibliographie

• [1] George Biddell Airy, On the Occultations of the Star Antares (alpha Scorpii) in 1856, Monthly Notices of the Royal Astronomical Society, 16, 1856, p.56
• [2] George Biddell Airy, On the Apparent Projection of Stars upon the Moon's Disk in Occultations, Monthly Notices of the Royal Astronomical Society, 19, 1859, p.208: « the integral which determines the brightness is so unmanageable that I am unable at present to assign the numerical values of the brightness at different distances from the geometrical outline »
• [3] A. Arnulf, Sur une méthode pour la mesure des diamètres apparents des étoiles,Comptes Rendus de l'Académie des Sciences, 202, 1936, p.115
• [4] Robert Burnham, Jr., Burnham's Celestial Handbook, Courier Dover Publications, Vol 3, 1979, p.1664 (descriptive notes), ISBN 0486236730
• [5] Arthur Stanley Eddington, Note on Major MacMahon's paper 'On the Determination of the apparent Diameter of a fixed Star' , Monthly Notices of the Royal Astronomical Society, 69, 1909, p.178
• [6] D. S. Evans, Photoelectric observations of lunar occultations. XV, Astronomical Journal, 90, 1985, p.2360
• [7] Alexander von Humboldt, A Sketch of a Physical Description of the Universe, vol. IV, Harper & brothers, New York, 1860, p.148
• [8] Major P. A. MacMahon , On the Determination of the apparent Diameter of a fixed Star, Monthly Notices of the Royal Astronomical Society, 69, 1908, p.126
• [9] B. D. Mason, Occultation Binaries Catalog, Publications of the Astronomical Society of the Pacific, 107, 1995, p.299
• [10] Simon Newcomb, Appendix II - Researches in the motion of the Moon, Astronomical and Meteorological Observations made at the U.S. Naval Observatory, 15, 1878, rapporte p. 77: From Astronomica Philolaica, p. 159, « Anno 1623 Julij die 5 cum Lunae centrum altum esset g. 17 1/3 Parisiis observavi occultationem Spicae Virginis à (Lune) »
• [11] Andrea Richichi, Lunar occultations: from past to future achievements, dans Very high angular resolution imaging, Kluwer, 1994, p.71
• [12] Andrea Richichi, Combining Optical Interferometry with Lunar Occultations, dans Spectroscopically and Spatially Resolving the Components of the Close Binary Stars, ASP Conference Series, 318, 2004, p.148
• [13] Nathaniel M. White, Stellar Multiplicity Discovery By Lunar Occultations dans Complementary Approaches to Double and Multiple Star Research, ASP Conference Series, 32, IAU Colloquium 135, 1992, p. 486
• [14] Nathaniel M. White, Lunar Occultations - from Conjecture to Results, Vistas in Astronomy, 30, 1987, pp.13

Voir aussi

Liens internes

• Étoile double visuelle
• Étoiles binaires, étoiles doubles

Liens externes

• Théorie_de_la_diffraction
• The International Occultation Timing Association
• La double planète Pluton-Charon rencontre une étoile triple
• La détection d’étoiles doubles serrées par les occultations lunaires
• Prédiction, observation et réduction des occultations stellaires de l'Institut de Mécanique Céleste et de Calcul des Éphémérides.

Portail Astronomie – Accédez aux articles de Wikipédia concernant l'astronomie.